
椭圆的第二定义:设动点M(x, y)与定点F(c, 0)的距离和它到定直线l: x=a2/c的距离的比是常数(a>c>0),则点M的轨迹是椭圆。点F是椭圆的一个焦点,直线l是椭圆中对应于焦点F的准线。常数e=c/a(0)。具体操作如下:
比如要制作一个端点固定,另一个端点在一个定圆上运动的线段中点的轨迹动画,操作流程如下:
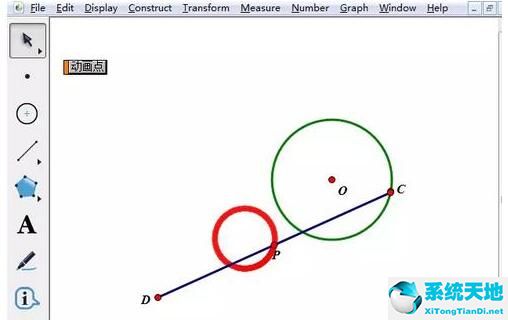
画出定圆O和线段DC,D是顶点,C是动点。选择左侧侧边栏“圆工具”在画板上任意画一个圆,圆心为O;选择“线段工具”画线段DC,D是顶点,C是动点,
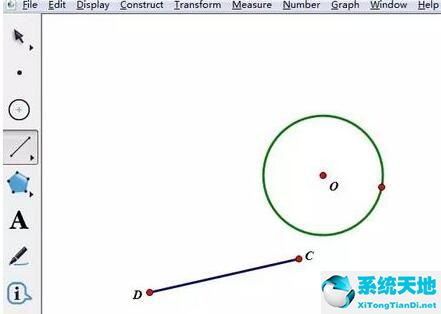
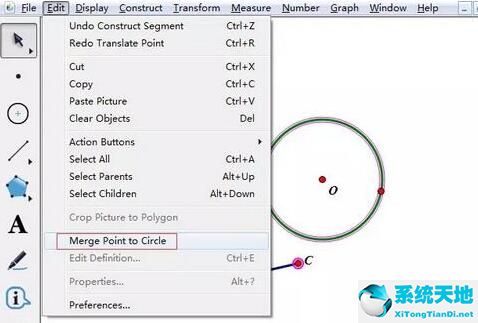
步骤二 选中圆O和点C,单击上方菜单栏“编辑”——“合并点到圆”,这样就能够保证点C运动时,始终在圆上。
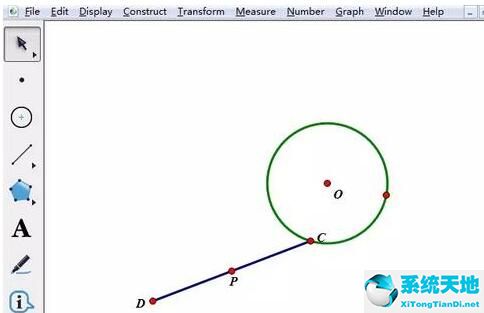
构造线段中点。选中选段CD,单击上方菜单栏“构造”——“中点”,得到线段中点,利用标签工具给中点打上标签P。
制作操作按钮。选中点C,注意不能选中圆,单击上方菜单栏“编辑”——操作类按钮——动画,在弹出的对话框运动速度,方向默认,点击“确定”。这时工作区多了个按钮。这时候,你若单击按钮,点C就在圆上动起来了,但点P还没留下轨迹。
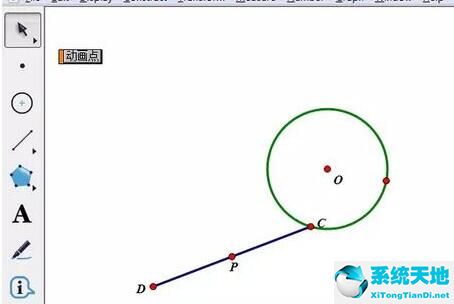
追踪中点。使用“移动工具”选中点P,单击上方菜单栏“显示”——“追踪中点”,
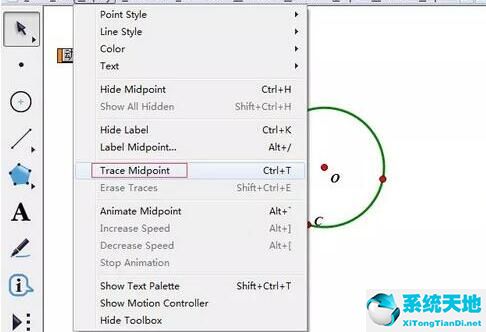
单击“动画点”按钮,很显然,可以看出点P的轨迹是一个圆。在运动过程中,按下按钮就能随处停止,再按一下又开始移动。这样演示动画就非常完美了。
相信现在看了上面的内容后,大家都了解了吧,希望对大家有帮助哦!